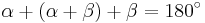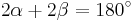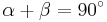Thales' theorem

For the theorem sometimes called Thales' theorem and pertaining to similar triangles, see Intercept theorem.

In geometry, Thales' theorem (named after Thales of Miletus) states that if A, B and C are points on a circle where the line AC is a diameter of the circle, then the angle ABC is a right angle. Thales' theorem is a special case of the inscribed angle theorem. It is generally attributed to Thales, who is said to have sacrificed an ox in honor of the discovery, but sometimes it is attributed to Pythagoras.

Contents

Proof

We use the following facts:

Let O be the center of the circle. Since OA = OB = OC, OBA and OBC are isosceles triangles, and by the equality of the base angles of an isosceles triangle, OBC = OCB and BAO = ABO. Let α = BAO and β = OBC. The three internal angles of the ABC triangle are α, α + β and β. Since the sum of the angles of a triangle is equal to two right angles, we have

\alpha%2B\left( \alpha %2B \beta \right) %2B \beta = 180^\circ

then

{2}\alpha %2B {2}\beta =180^\circ

or simply

\alpha %2B \beta =90^\circ

Q.E.D.

Converse

The converse of Thales' theorem is also valid; it states that a right triangle's hypotenuse is a diameter of its circumcircle.

Combining Thales' theorem with its converse we get that:

The center of a triangle's circumcircle lies on one of the triangle's sides if and only if the triangle is a right triangle.

Proof of the converse using geometry

This proof consists of 'completing' the right triangle to form a rectangle and noticing that the center of that rectangle is equidistant from the vertices and so is the center of the circumscribing circle of the original triangle, it utilizes two facts:

Let there be a right angle ABC, r a line parallel to BC passing by A and s a line parallel to AB passing by C. Let D be the point of intersection of lines r and s (Note that it has not been proven that D lies on the circle)

The quadrilateral ABCD forms a parallelogram by construction (as opposite sides are parallel). Since in a parallelogram adjacent angles are supplementary (add to 180°) and ABC is a right angle (90°) then angles BAD, BCD, and ADC are also right (90°); consequently ABCD is a rectangle.

Let O be the point of intersection of the diagonals AC and BD. Then the point O, by the second fact above, is equidistant from A,B, and C. And so O is center of the circumscribing circle, and the hypotenuse of the triangle AC is a diameter of the circle.

Proof of the converse using linear algebra

This proof utilizes two facts:

Let there be a right angle ABC and circle M with AC as a diameter. Let M's center lie on the origin, for easier calculation. Then we know

It follows

0 = (A − B) · (B − C) = (A − B) · (B + A) = |A|2 − |B|2.

Hence:

|A| = |B|.

This means that A and B are equidistant from the origin, i.e. from the center of M. Since A lies on M, so does B, and the circle M is therefore the triangle's circumcircle.

The above calculations in fact establish that both directions of Thales' theorem are valid in any inner product space.

Generalization

Thales' theorem is a special case of the following theorem:

Given three points A, B and C on a circle with center O, the angle AOC is twice as large as the angle ABC.

See inscribed angle, the proof of this theorem is quite similar to the proof of Thales' theorem given above.

Application

Thales' theorem can be used to construct the tangent to a given circle that passes through a given point. (See figure.) Given a circle k, with a center O, and a point P outside of the circle, we want to construct the (red) tangent(s) to k that pass through P. Suppose the (as yet unknown) tangent t touches the circle in the point T. From symmetry, it is clear that the radius OT is orthogonal to the tangent. So construct the midpoint H between O and P, and draw a circle centered at H through O and P. By Thales' theorem, the sought point T is the intersection of this circle with the given circle k, because that is the point on k that completes a right triangle OTP.

Since there the two circles intersect at two points, we can construct both tangents in this fashion.

History

Thales was not the first to discover this theorem since the Egyptians and Babylonians must have known of this empirically, however there is no record of a proof of the theorem by either of them. The theorem is named after Thales because he was said to have been the first to prove the theorem, using his own results that the base angles of an isosceles triangle are equal, and that the sum of angles in a triangle is equal to two right angles.

See also

References

External links